Computer Graphics - Viewing Transformation include the following topics: View / Camera Transformation and Projection Transformation.

---

CG-Viewing Transformation

View Transformation

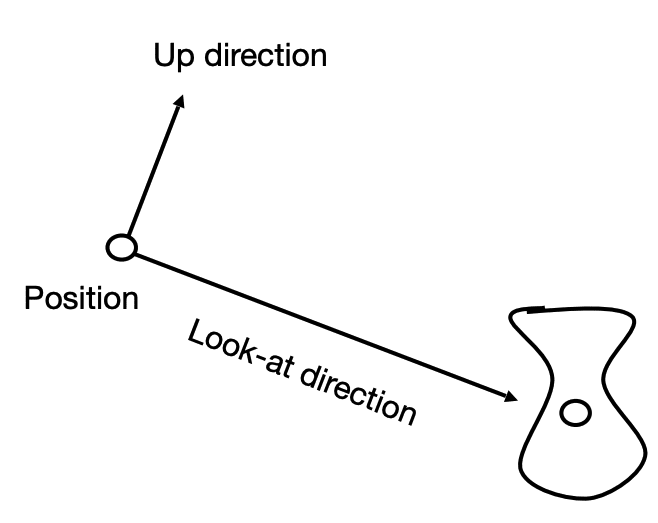
• Define the camera first
  • Position $\overrightarrow{e}$
  • Look-at / gaze direction $\overrightarrow{g}$
  • Up direction $\hat{t}$ (assuming perpendicular to look-at)

Key observation

If the camera and all objects move together, the “photo” will be the same.

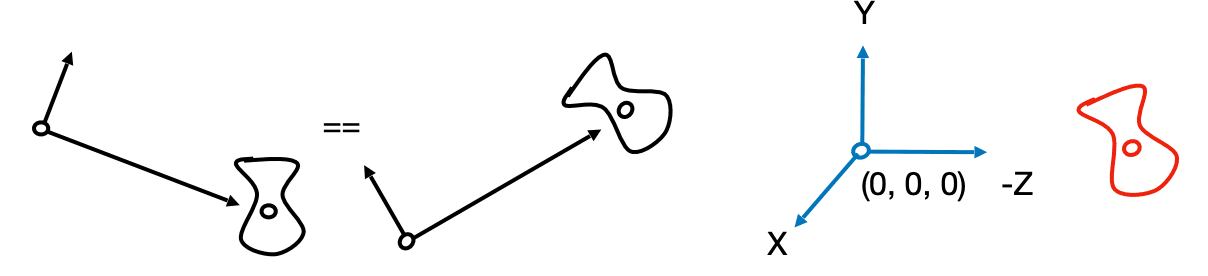
How about that we always transform the camera to

• The origin, up at $Y$, look at $-Z$
• And transform the objects along with the camera

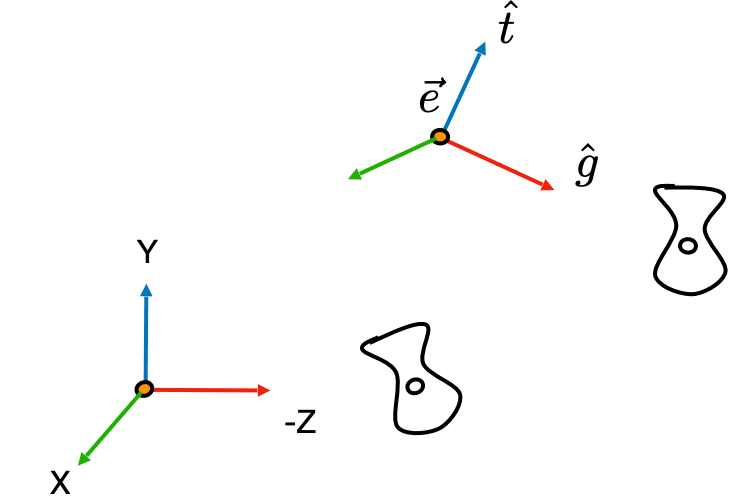
• $M_{\text{view}}$ in math?

  • Translates $\overrightarrow{e}$ to origin
  • Rotates $\overrightarrow{g}$ to $-Z$
  • Rotates $\overrightarrow{t}$ to $Y$
  • Rotates $(\overrightarrow{g}\times \overrightarrow{t})$ to $X$
  • Difficult to write!

• $M_{\text{view}}$ in math?

  • Let's write $M_{\text{view}}=R_{\text{view}}{T}_{\text{view}}$
    • Translate $\overrightarrow{e}$ to origin:
      $T_{\text{view}}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$
    • Rotate $\overrightarrow{g}$ to $-Z$, $\overrightarrow{t}$ to $Y$, $(\overrightarrow{g}\times \hat{t})$ to $X$
  • Consider its inverse rotation: $X\to (\overrightarrow{g}\times \hat{t}),Y\to \hat{t},Z\to -\overrightarrow{g}$

$$R_{\text{view}}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_{\hat{t}}& x_{-\overrightarrow{g}}& 0\\ y_{\hat{g}\times \hat{t}}& y_{\hat{t}}& y_{-\overrightarrow{g}}& 0\\ z_{\hat{g}\times \hat{t}}& z_{\hat{t}}& z_{-\overrightarrow{g}}& 0\\ 0& 0& 0& 1\end{array}\right]$$$$R_{\text{view}}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_{\hat{t}}& y_{\hat{t}}& z_{\hat{t}}& 0\\ x_{-\overrightarrow{g}}& y_{-\overrightarrow{g}}& z_{-\overrightarrow{g}}& 0\\ 0& 0& 0& 1\end{array}\right]$$

Also Known as ModelView Transformation

Projection Transformation

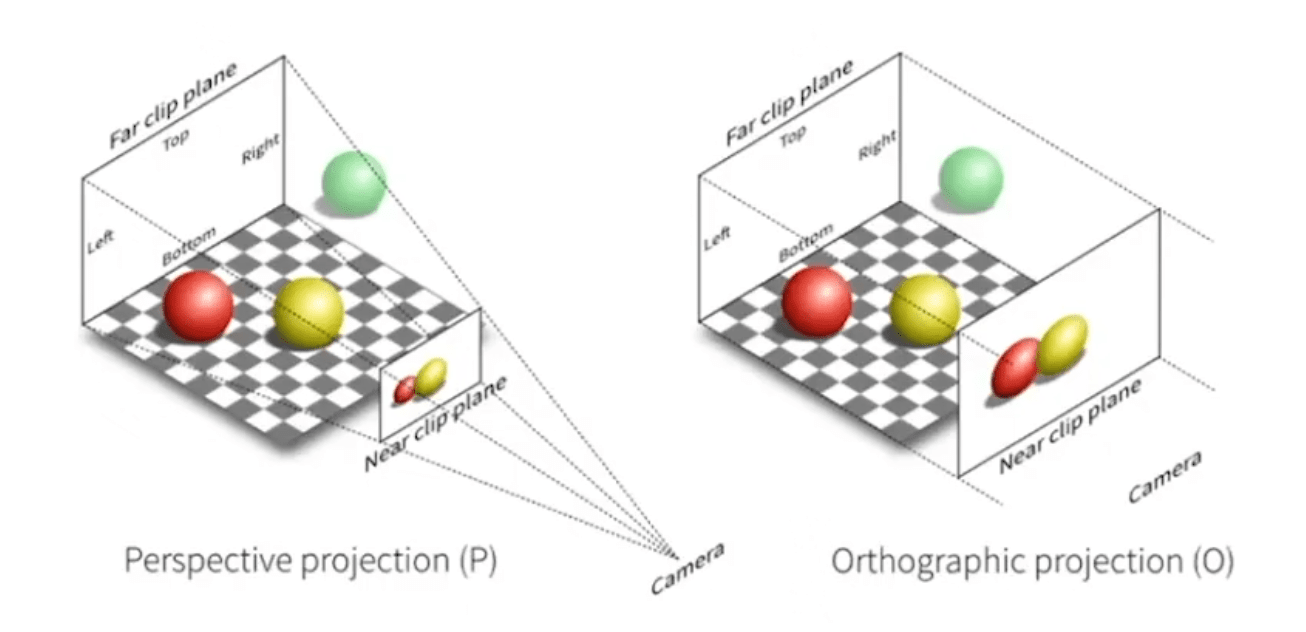
Orthographic Projection

• A simple way of understanding

  • Camera located at origin, looking at $-Z$, up at $Y$
  • Drop $Z$ coordinate
  • Translate and scale the resulting rectangle to $[-1,1{]}^2$

• In general

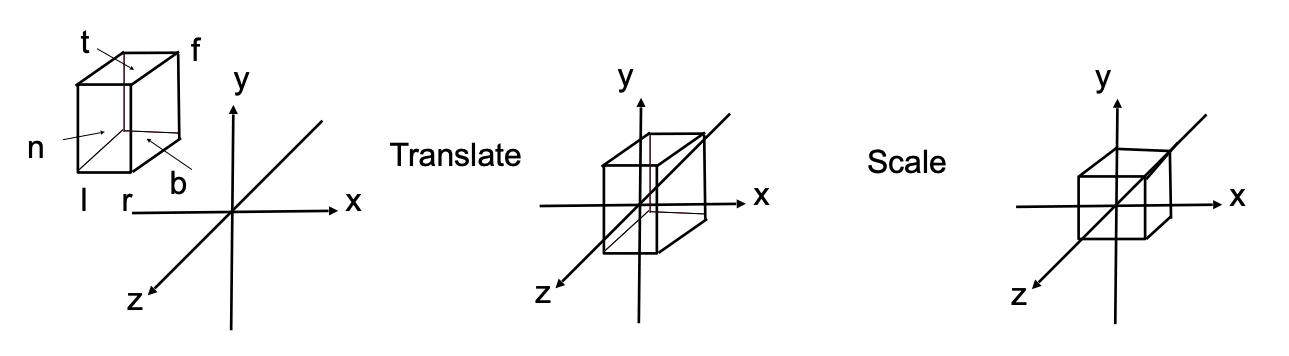
  • We want to map a cuboid $[l,r]\times [b,t]\times [f,n]$
    to the "canonical" (正则, 规范, 标准) cube $[-1,1{]}^3$.

• Transformation matrix

  • Translate (center to origin) first, then scale (length/width/height to 2)
  $$M_{\text{ortho}}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

Perspective Projection

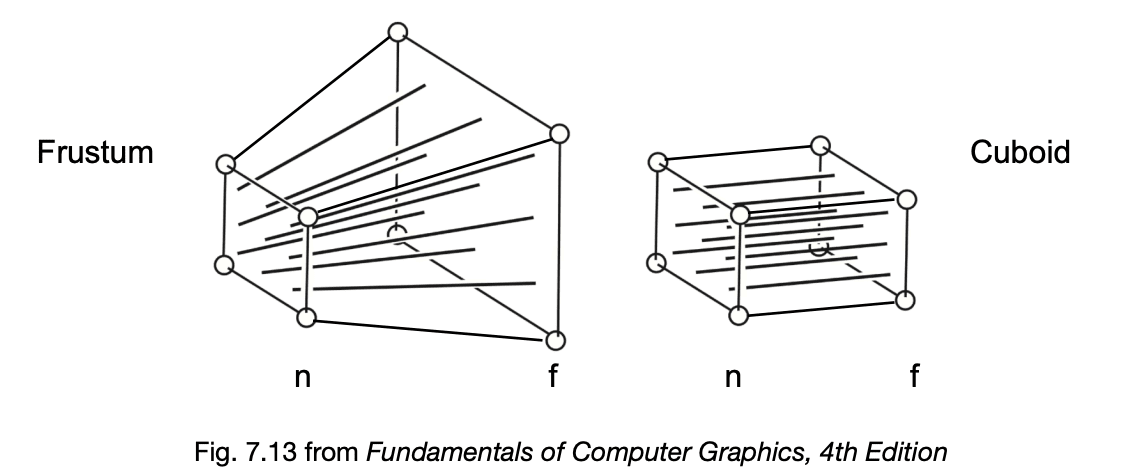
• How to do perspective projection
  • First "squish" the frustum into a cuboid ($n\to n,f\to f$) ($M_{\text{persp}\to \text{ortho}}$)
  • Do orthographic projection ($M_{\text{ortho}}$, already known!)

• In order to find a transformation

  • Find the relationship between transformed points ($x^{\prime },y^{\prime },z^{\prime }$)
    and the original points ($x,y,z$):
  $$y^{\prime }=\frac{n}{z}y{x}^{\prime }=\frac{n}{z}x(\text{similar to }{y}^{\prime })$$

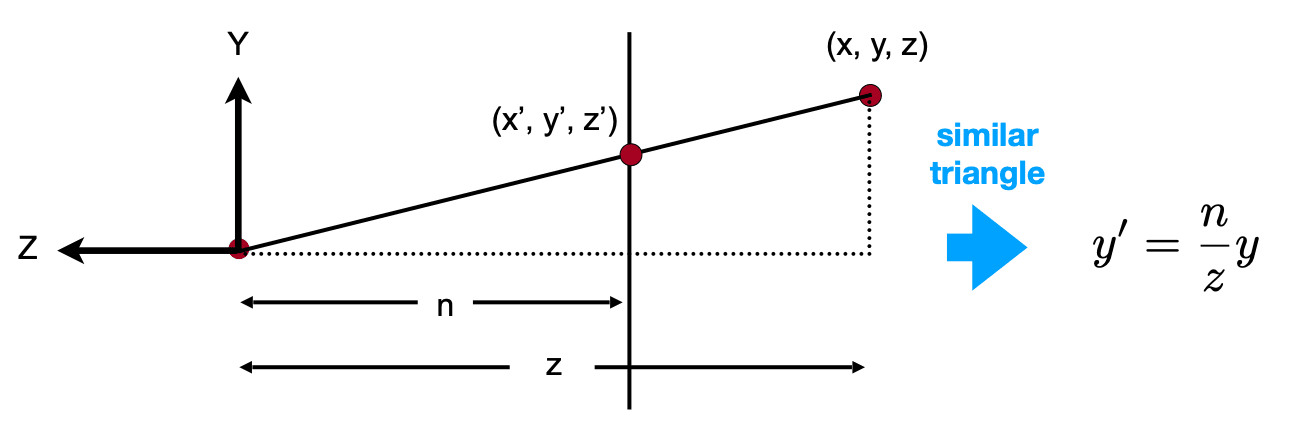
• In homogeneous coordinates,

$$\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)⟹\left(\begin{array}{c}\frac{nx}{z}\\ \frac{ny}{z}\\ \text{unknown}\\ 1\end{array}\right)\text{(mult. by }z\text{)}==\left(\begin{array}{c}nx\\ ny\\ \text{still unknown}\\ z\end{array}\right)$$

• So the "squish" (persp to ortho) projection does this

$$M_{\text{persp}\to \text{ortho}}^{(4\times 4)}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ \text{unknown}\\ z\end{array}\right)$$

• Already good enough to figure out part of $M_{\text{persp}\to \text{ortho}}$:

$$M_{\text{persp}\to \text{ortho}}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right)$$

• Observation: the third row is responsible for $z^{\prime }$

  • Any point on the near plane will not change
  • Any point’s $z$ on the far plane will not change

• Any point on the near plane will not change

$$M_{\text{persp}\to \text{ortho}}^{(4\times 4)}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ \text{unknown}\\ z\end{array}\right)\text{(replace }z\text{ with }n\text{)}\Rightarrow \left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right)$$

• So the third row must be of the form $(00AB)$

$$(00AB)\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=n^2{n}^2\text{ has nothing to do with }x\text{ and }y$$

• Any point’s $z$ on the far plane will not change

$$\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right)$$$$Af+B=f^2$$

• Solve for $A$ and $B$:

$$An+B=n^2$$$$Af+B=f^2$$$$\Rightarrow A=n+f,B=-nf$$

• Finally, every entry in $M_{\text{persp}\to \text{ortho}}$ is known!

$$M_{\text{persp}\to \text{ortho}}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right)$$

• What’s next?
  • Perform orthographic projection ($M_{\text{ortho}}$) to finish.
  • Combine transformations:$$M_{\text{persp}}=M_{\text{ortho}}\cdot M_{\text{persp}\to \text{ortho}}$$

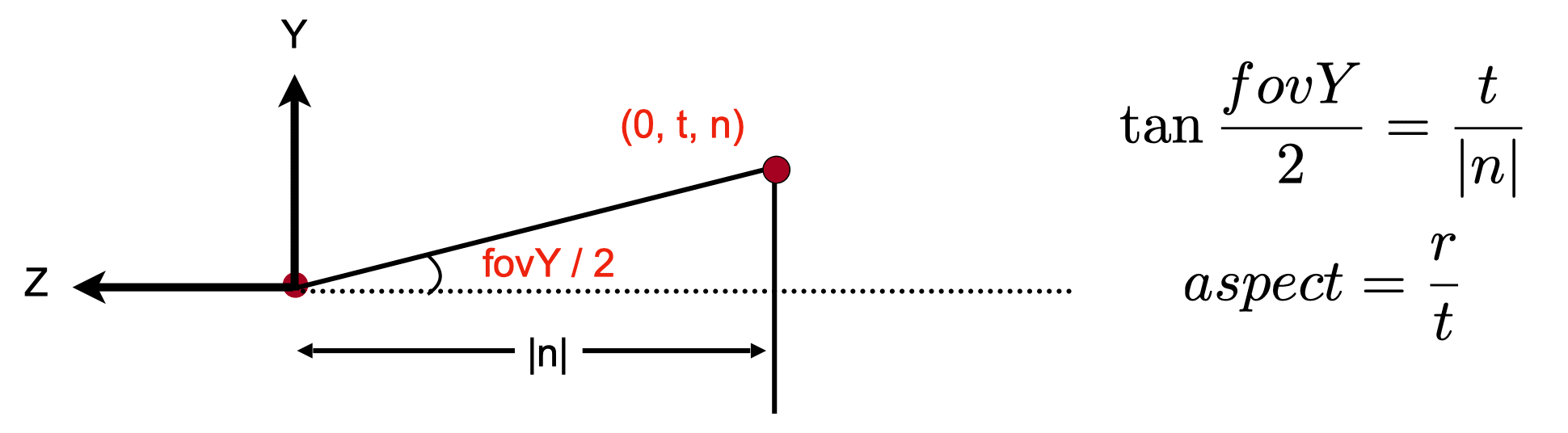
Vertical field-of-view (fovY)

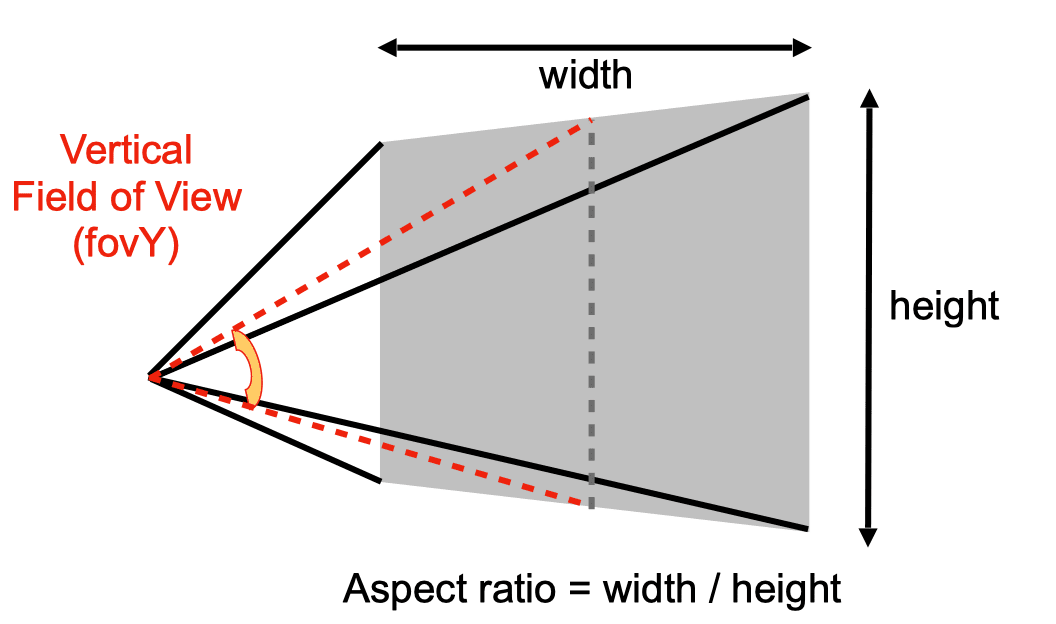
How to convert from fovY and aspect to $l,r,b,t$?